測驗M06

編碼與解碼，是個有名的問題，可以應用在壓縮或是安全系統中，現在假設有一個編碼系統是「乘2加1」，當然，若要作解碼，則是「減1後再除2」，例如某個英文字母A, 因為他的ASCII的編碼是65, 所以乘2加1後，就變為131，同理：英文字母C, 因為他的ASCII的編碼是67, 所以乘2加1後，就變為135，而英文字母b編碼後變為197。

先是一個整數N，代表以下有N個樣本，接下來是N行測試的輸入樣本，每行是一個大寫或是小寫的英文字母。

旅美球星王建民，首度在美國職棒大聯盟上場，是對上多倫多藍鳥隊，表現沉穩，幾度化險為夷，充份表現大將之風。洋基最終以4:3險勝藍鳥，雖然，結果王建民無勝負記錄，但是他的整體表現已算不錯。第二場比賽，是對上魔鬼魚，一上場，王建民就手軟，面對第一棒投出4壞保送，結果在後來的盜疊及安打中，先失1分！直到投完六局才換上中繼投手，雖然只被打出八支安打，但是失了5分！不過王建民的首度大聯盟三振也終於出爐，而且總共三振了3名球員，後來由於打擊火力不夠，終場以2：6敗陣，王建民只好吞下第一場敗投。讓我們繼續為中華健兒的表現加油！

現在如果在賽前，可預知投手的配球，且假設打擊都不會打出安打，那單純由好球與壞球的配球來判斷到底球賽的結果如何？我們用O表好球。用X表壞球，而且是只要累計達3個好球(O)，就算一人出局，或累計達4壞球(X)，就一人上疊，請問看到所有的配球後，可知已幾次四壞保送，又有幾次三振出局呢？要注意的是，若已累計達3好，或是4壞，則要重計算，而且最後未成三好或四壞則忽略之。例如：

OOXXOOOOXXXOXOXXOOè OOXXO(3好)OOO(3好)XXXOX(4壞)OXXOO(3好)
è結果是3人出局(Out)，1人保送(Free)。輸出結果是：3Out,1Free

OXXOXXOXOXXOOè OXXOXX(4壞)OXOXXO(3好)O(未知)
è結果是1人出局(Out)，1人保送(Free)。輸出結果是：1Out,1Free

有很多的輸入樣本，每行代表一個樣本。每個樣本是連續的O與X的組合。(組合的長度<100)。

每個樣本就有一行的輸出，必須包含兩個數字，分別代表出局與保送的人數

由於電子產品進步很快，所以近來DVD錄放影機的價格也越來越平價。若有某一台DVD錄放影機，有不錯的單鍵錄影功能，也就是在選好電視的電台訊號後，只要按一下「錄影」鍵即可開始錄影，但為了配合一般的節目大都是30、60、90、120分鐘的習慣，所以有了快速錄節目的設計，就是在開始錄後，只要重覆再按「錄影」按鍵一下，則自動設定錄影結束時間在30分鐘後，若是連按兩下「錄影」鍵，則是60分鐘後自動停止。同理，若是3下，則是90分，4下則是120分…假設錄影時間可以很長，則設定的錄影時間也就可以很久哦！

有很多的輸入樣本，每兩行代表一個樣本。每個樣本的第一行是時間，代表按「錄影」的時間。下一行是一個數字，若0，代表不設停止時間。若1，則依上述，表示錄影30分鐘，依此類推(最大不會超過10)。假設，錄影的時限不會有問題。但要注意若錄影時間超過午夜12點的情形！

每個樣本就有一行的輸出，是一個代表自動停止錄影的時間。若0，因為代表不設停止時間，所以停止的時間未知，所以請印出????????八個問號來代表。

????????

2005/2/28 22:42:51

2005/3/1 0:12:51

今年(九十四學年度) 四技二專統一入學測驗比去年晚，定在5/14．5/15 。現在以去年(九十三學年度)的統計表，作個簡單的預測：若有某位考生，已得知數學(Math)的分數，請問在全國排名上，已經可確定落後至少有多少人了呢？例如若得分是100分則是0人。96分則是1039，88分則是3870人，40分則是7277人。請參考附表，自行選擇有用的資訊，完成這個專案。

先是一個整數N, 代表有N位同學，要作成績的落點預測。接下來的N行，是每行代表一個樣本，每樣本就是由一個數字組成。

每個樣本就有一行的輸出，是一個代表可確定至少會落後的人數。

輸入N個1~1000的整數，請由「可被9整除的奇數」中，找出最大的數。例如：9,18,12,5,27,30,63,1,5,6則請印出63. 例如：36,7,6,72則請印出”Not Foound”，代表沒有發現符合題意的數字。

有很多的輸入樣本，每兩行代表一個樣本。第一行是一個整數N，代表下一行中，將會有N個整數的資料。不會有不合理的輸入。若N=0表示結束輸入。

請依題意印數字，或是”Not Found”即可。每個樣本請印在一行。

圍棋中有很多有用的術語，常見的就是「碰來扳」，但是，扳的方向有上扳、下扳。所謂的上或下，我們將棋盤的四邊視為下面，而棋盤的中心點稱為「天元」，也就是上面。現在已知黑棋已有一子落在某個座標上，若再知道白子碰黑子的座標，請印出上扳的座標。

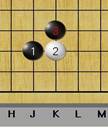
關於棋盤座標的指定方式，垂直方向由下而上，編為1到19，水平方向用大寫英文字母A到T(※略過I不用)，所以左下角視為原點用(A,1)代表，右下角用(T,1)來代表，右上角，則是(T,19)來代表。所以如果「黑棋1」的座標在(D,3)，而如果「白棋2」在(E,3)的地方碰白子，則「白子3」要上扳座標就是在(E,4)，如圖I所示；其他的例子中，都是先有黑棋1，然後白棋2去碰後，黑棋3就是要印的座標。

有很多的輸入樣本，每一行代表一個樣本。每個樣本是由兩個分別代表「黑棋1」，「白棋2」的座標，兩個座標只用逗號隔開。座標不會有不合理的輸入。也不會有模糊不清的情形。樣本中：R,16,Q,16的上扳應該是Q,15，但為了簡化問題，所輸入的座標，垂直方向，將不會有大於9的情形，而且白棋2，碰黑棋1時，必然只在他的左邊或是右邊，所以只要注意水平方向的變化即可解決此題。

E, 4

C, 4

K, 4

R, 4

E, 5

某地區因乾旱，自來水公司擬於下週日至下週六的7天中選2天停止供水。為了避免造成民眾太大的不方便，所以要求停水的兩天不可以相連，則自來水公司有幾種選擇方式？我們在此用1代表星期1，2代表星期2，7代表星期日。則可能的方式為：13,14,15,16,17,24,25,26,27,35,36,37,46,47,67等15種情形。現在為了配合缺水情況的不同，請寫一個程式來幫水公司的主管，快速了解全部的情形。
例如：若要在5天內安排的方式只有13,14,15,24,25,35等6種情形。

有很多的輸入樣本，每樣本一行，每行只有一個整數數字N(3<=N <=30)，表示要安排停水的天數。

每個樣本都有兩行的輸出，第一行是一系列由小到大排，而且是所有可能兩天不相連的情形。而且如果日期大於10 以上，則第10天用A代表，11天用B代表，…第19天用J代表，依此類推。第二行則是先印出”Count=”然後是所有可能的情形的總數。

13,14,15,16,17,18,19,1A,1B,1C,1D,1E,1F,1G,1H,24,25,26,27,28,29,2A,2B,…<略>…,DF,DG,DH,EG,EH,FH,

13,14,15,16,17,18,19,1A,1B,1C,1D,1E,1F,1G,1H,1I,1J,1K,1L,1M,…<略>…,QS,QT,QU,RT,RU,SU,

Count= 406

小瓜呆是一位學校的學生，由於學校課業較多，而他又熱心又求好心切，常常會很多件事情都要在一天內完成。但是他知道，「信用」是很重要的，而且同一時間，只適合作好一件事，或是讀好一種課程。為了讓所有的事情都可以在時限內順利完成，所以希望請你幫他設計程式，來協助這些事情的安排。他有一個習慣，那就是每天晚上都會收集明天要完成的事與進度，當然每件事所花的時間不同，要完成的截止時間也不同。為了維持信用，所以小瓜呆希望可以在晚上就知道明天的工作是否可以順利完成，若不能全部完成，則要事先主動告知相關工作的負責人。你能幫小瓜呆寫好這個程式，在前晚就知明天是否可以全部完工？若無法全部完工，也可以一大早先作好緊急處理來維持個人的信用。

有多個樣本，一開始的第一行代表共有多少個樣本M, 然後每個樣本的第一行是一個整數數字N(1<=N <20)，表示要安排的工作數。接下來的若干行代表有N項工作，每項工作將剛好有三個整數數字，分別代表要處理的工作代號、工作時間與該工作必需完成的截止時間。

對於每個樣本要輸出是「Yes」代表可全部完工，或「No」代表相反。如果是Yes，則還必需在加上「:」後，並顯示可以作完全部工作的工作代號。必須按先後的順序，由先作到最後作。

共同科目-數學(Math) 成績人數累計表
分數區間	人數	百分比累計	人數累計	百分比
96.01-100.00	1039	0.90%	1039	0.90%
92.01-96.00	1271	1.10%	2310	2.00%
88.01-92.00	1560	1.35%	3870	3.35%
84.01-88.00	1629	1.41%	5499	4.76%
80.01-84.00	1778	1.54%	7277	6.30%

圖 I	圖II	圖III	圖IV	圖V	圖VI(僅供參考)

印出E,4	印出C,4	印出K,4	印出R,4	印E,5	印出Q,15